| Name | Type | Description | #Solved | #Total |
| BPP FLK | BPP | 1D Bin-Packing Problems from FALKENAUER (1996). | 160 | 160 |
| CSP FLK | CSP | 1D Bin-Packing Problems from FALKENAUER (1996) [demand x 10^6]. | 160 | 160 |
| Fiber | CSP | Instances taken from a real application in a paper tube industry in Japan. | 39 | 39 |
| Cutgen | CSP | CUTGEN (Gau and Wascher, 1995). | 1800 | 1800 |
| 1D-bar | CSP | 1D-bar relaxations of the two-dimensional bin packing test dataset of Lodi et al. (1999). | 500 | 500 |
| Scholl | BPP | 1D Bin-Packing Problems from SCHOLL/KLEIN/JUERGENS (1997). | 1210 | 1210 |
| Hard28 | BPP | The 28 VERY hard BPP instances of J. Schoenfield (with m from 140 to 200). | 28 | 28 |
| SCH/WAE | BPP | 1D Bin-Packing Problems from SCHWERIN/WAESCHER (1998). | 200 | 200 |
| WAE/GAU | BPP | 1D Bin-Packing Problems from WAESCHER/GAU (1996). | 17 | 17 |
| 2CBP | 2CBP | Two-Constraint Bin Packing instances of Spieksma/Caprara/Toth. | 330 | 400 |
| 20CBP | VBP | 20-dimensional vector packing instances based on the 2CBP dataset of Spieksma/Caprara/Toth. | 33 | 40 |
| 0-1 CSP FLK | 0-1 CSP | 1D Bin-Packing Problems from FALKENAUER (1996) [demand x 10^6; with binary patterns]. | 160 | 160 |
| 0-1 Fiber | 0-1 CSP | Instances taken from a real application in a paper tube industry in Japan [with binary patterns]. | 39 | 39 |
| 0-1 Cutgen | 0-1 CSP | CUTGEN (Gau and Wascher, 1995) [with binary patterns]. | 1800 | 1800 |
| 0-1 1D-bar | 0-1 CSP | 1D-bar relaxations of the two-dimensional bin packing test dataset of Lodi et al. (1999) [with binary patterns]. | 500 | 500 |
| BPPC | BPPC | BPP w/ Conflicts Problems from Muritiba et al. (2010). | 800 | 800 |
| BPPC_CS | 0-1 CSP FP | CSP w/ binary patterns and forbidden patterns based on the BPPC dataset of Muritiba et al. (2010). | 800 | 800 |
| Card BPP FLK | BPP Card | 1D Bin-Packing Problems from FALKENAUER (1996) [with cardinality constraints]. | 320 | 320 |
| Card CSP FLK | CSP Card | 1D Bin-Packing Problems from FALKENAUER (1996) [demand x 10^6; with cardinality constraints]. | 320 | 320 |
| Card Fiber | CSP Card | Instances taken from a real application in a paper tube industry in Japan [with cardinality constraints]. | 279 | 279 |
| Card Cutgen | CSP Card | CUTGEN (Gau and Wascher, 1995) [with cardinality constraints]. | 7299 | 7299 |
| Card 1D-bar | CSP Card | 1D-bar relaxations of the two-dimensional bin packing test dataset of Lodi et al. (1999) [with cardinality constraints]. | 1415 | 1415 |
| Card Scholl | BPP Card | 1D Bin-Packing Problems from SCHOLL/KLEIN/JUERGENS (1997) [with cardinality constraints]. | 3748 | 3748 |
| Card Hard28 | BPP Card | The 28 VERY hard BPP instances of J. Schoenfield (with m from 140 to 200) [with cardinality constraints]. | 56 | 56 |
| Card SCH/WAE | BPP Card | 1D Bin-Packing Problems from SCHWERIN/WAESCHER (1998) [with cardinality constraints]. | 1000 | 1000 |
| Card WAE/GAU | BPP Card | 1D Bin-Packing Problems from WAESCHER/GAU (1996) [with cardinality constraints]. | 131 | 131 |
| Graph Coloring | Coloring | Some graph coloring instances from OR-Library | 4 | 4 |
| Timetabling | Timetabling | "hard timetabling" instances from OR-Library | 5 | 5 |
|
| Label | Description |
| Wi | bin capacity on the i-th dimension |
| C | cardinality limit |
| M | number of different item types |
| N | number of items |
| NDIMS | number of dimensions/constraints |
| ZIP | optimum objective value |
| ZLP | linear relaxation lower bound |
| TPRE | time spent in pre-processing (seconds) |
| TLP | time spent in the linear relaxation of the root node (seconds) |
| NN | number of nodes explored in the branch-and-bound procedure |
| TIP | time spent in the branch and bound procedure (seconds) |
| TTOT | total run time (seconds) |
| VF | number of vertices in the final graph |
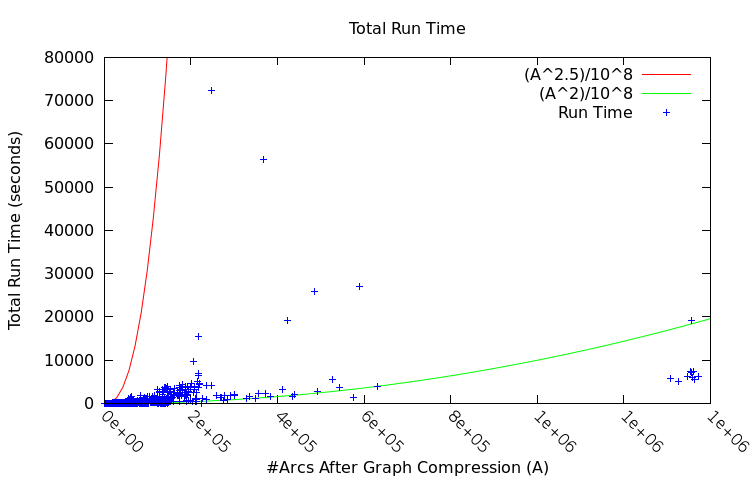
| AF | number of arcs in the final graph |
| RV | percentage of vertices removed by the graph compression [1-(#vertices w/ graph compression)/(#vertices w/o graph compression)] |
| RA | percentage of arcs removed by the graph compression [1-(#arcs w/ graph compression)/(#arcs w/o graph compression)] |
|